6.2 Real Integrating Spheres

Due to the simplifications assumed for an ideal integrating sphere, the relations derived in “Theory of the ideal integrating sphere” cannot be applied directly in practical applications. They have to be altered for the following reasons:

• The reflectance ρ might depend on wavelength. This results in a wavelength dependent sphere multiplier K and thus in a spectral distortion of the primary source’s output. As a result, the relations for the ideal sphere, which have been formulated for radiometric quantities, can no longer be applied directly. The sphere’s behavior for monochromatic radiation has to be determined by considering the respective relations for spectral radiometric quantities. If desired, radiometric quantities describing the sphere’s radiation output can be determined by subsequent wavelength integration of the respective spectral radiometric quantities.

• Intensity considerations pose a lower limit for the size of the entrance and exit ports because the radiant power entering or exiting a sphere is proportional to the area of the respective port. As a result, these ports might reduce the amount of light reflected at the sphere’s inner surface considerably. This can be accounted for by a modified sphere multiplier:

Etotal =	Φ0	×	ρ	=	Φ0	× K
	Asphere		1 - ρ (1 - a)		Asphere

with

K =	p
	1 - ρ (1 - a)

In these relations, α denotes the relative share of the area of all ports and other non-reflecting areas on the sphere’s total inner surface:

a =	sum of all non-reflecting areas
	Asphere

The figure below shows the dependence of the sphere multiplier on reflectance ρ for different values of a. It can be noted that even a small variation of reflectance might cause significant change in the sphere multiplier.

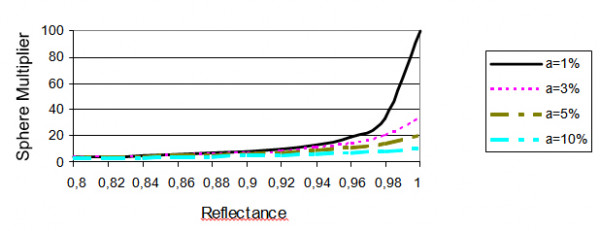
Fig. 1: Dependence of the sphere multiplier K on reflectance ρ for different values of the share of nonreflecting areas on the sphere’s total inner surface

For this reason, a slight wavelength dependency of ρ may result in a strong wavelength dependency of the sphere multiplier.

• Objects inside the sphere, for example the light source itself, cannot generally be neglected in their influence on the reflected optical radiation. A possible solution is the determination of the light source’s influence by means of an auxiliary lamp.

• Baffles inside the sphere and deviations of the coating material’s reflectance properties from perfect Lambertian reflection cause further deviations of the sphere’s behavior from the relations. Their influence can only be simulated by numerical Monte Carlo simulations, which basically use ray tracing techniques to follow the paths of a large number of individual photons.

Apart from these factors, integrating spheres are also subject to temporal variations of their optical properties, which are primarily caused by degradation of their coating material. In particular, the traditional coating material, Barium sulphate (BaSO₄), ages significantly when exposed to UV radiation.

Optically diffuse material (OP.DI.MA) is an optical grade plastic that is specially designed to work as a volume reflector. It has been designed to replace barium sulfate as a coating for integrating spheres in UV and high temperature applications. Its reflective properties depend on its thickness, generally specified at 10 mm which is the recommended minimum thickness for lighting engineering.

Apart from its temporal stability, OP.DI.MA offers additional advantages. Using different additives, its reflection factor can be adjusted to any value between 3 % (deep black) and 99 % (brilliant white), whereby uniform reflectance over a wide spectral range and over large geometrical areas can be achieved. Like other plastics, it can be processed by turning, drilling, sawing and milling and is available in raw blocks, plates and foils in various sizes for this purpose.