1.8 Reflection, Transmission and Absorption

Reflection is the process by which electromagnetic radiation is returned either at the boundary between two media (surface reflection) or at the interior of a medium (volume reflection), whereas transmission is the passage of electromagnetic radiation through a medium. Both processes can be accompanied by diffusion (also called scattering), which is the process of deflecting a unidirectional beam into many directions. In this case, we speak about diffuse reflection and diffuse transmission (Fig. 1). When no diffusion occurs, reflection or transmission of a unidirectional beam results in a unidirectional beam according to the laws of geometrical optics (Fig. 2). In this case, we speak about regular reflection (or specular reflection) and regular transmission (or direct transmission). Reflection, transmission and scattering leave the frequency of the radiation unchanged. Exception: The Doppler Effect causes a change in frequency when the reflecting material or surface is in motion.

Absorption is the transformation of radiant power to another type of energy, usually heat, by interaction with matter.

• For the optical measurement of reflection, transmission, absorption, and photoluminescence integrating sphere measuring systems are suitable.
• For the measurement of scattering samples we would like to refer to a spectrophotometer specially designed for this purpose.
• The measurement of classical transmission and reflection with a handheld device requires measuring systems with intelligent correction methods.

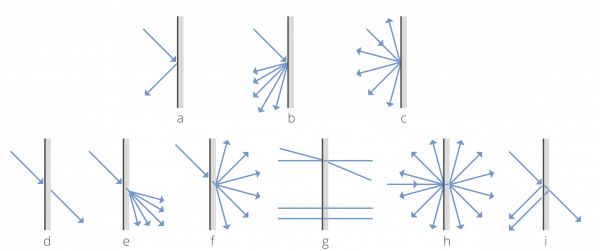
Fig. 1: top: Direct, mixed and diffuse reflection bottom: direct, mixed and diffuse transmission

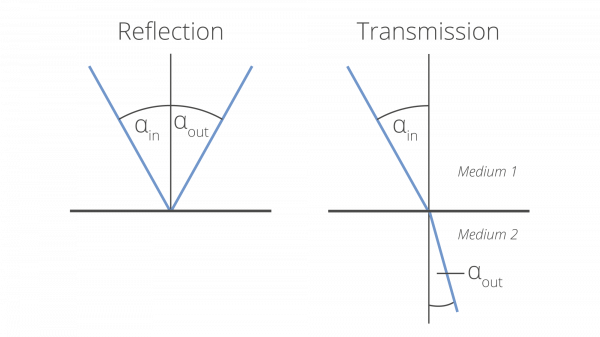
Fig. 2: When directly reflected or directly transmitted, a unidirectional beam follows the laws of geometrical optics:
direct reflection (left): αi_n = α_out, direct transmission (right): n₁ × sin(α_in) = n₂ × sin(α_out) with n₁ and n₂ denoting the respective medium’s index of refraction

Reflectance ρ, Transmittance τ and Absorptance α

In general, reflection, transmission and absorption depend on the wavelength of the affected radiation. Thus, these three processes can either be quantified for monochromatic radiation (in this case, the adjective “spectral” is added to the respective quantity) or for a certain kind of polychromatic radiation. For the latter, the spectral distribution of the incident radiation has to be specified. In addition, reflectance, transmittance and absorptance might also depend on polarization and geometric distribution of the incident radiation, which therefore also have to be specified.

The reflectance ρ is defined by the ratio of reflected radiant power to incident radiant power. For a certain area element dA of the reflecting surface, the (differential) incident radiant power is given by the surface’s irradiance E_e multiplied with the size of the surface element, thus

dΦ_e, incident = E_e dA

The (differential) reflected radiant power is given by the exitance M_e multiplied with the size of the surface element:

dΦ_{e, reflected} = M_e dA

Thus,

ρ =	dΦe, reflected	=	Me × dA	=	Me
	dΦe, incident		Ee × dA		Ee

or

M_e = ρ E_e

Total reflectance is further subdivided in regular reflectance ρ_r and diffuse reflectance ρ_d, which are given by the ratios of regularly (or specularly) reflected radiant power and diffusely reflected radiant power to incident radiant power. From this definition, it is obvious that

ρ = ρ_r + ρ_d

The transmittance τ of a medium is defined by the ratio of transmitted radiant power to incident radiant power. Total transmittance is further subdivided in regular transmittance τ_r and diffuse transmittance τ_d, which are given by the ratios of regularly (or directly) transmitted radiant power and diffusely transmitted radiant power to incident radiant power.

Again,

τ = τ_r + τ_d

The absorptance α of a medium is defined by the ratio of absorbed radiant power to incident radiant power.

Being ratios of radiant power values, reflectance, transmittance and absorptance are dimensionless.

Quantities such as reflectance and transmittance are used to describe the optical properties of materials. The quantities can apply to complex radiation or monochromatic radiation. The optical properties of materials are not a constant since they are dependent on many parameters such as:

• thickness of the sample

• surface conditions

• angle of incidence

• temperature

• the spectral composition of the radiation (CIE standard illuminants A, B, C, D65 and other illuminants D)

• polarization effects

The measurement of optical properties of materials using integrating spheres is described in DIN 5036-3 and CIE 130-1998.

Radiance coefficient q_e, Bidirectional reflectance distribution function (BRDF)

The radiance coefficient q_e characterizes the directional distribution of diffusely reflected radiation. In detail, the radiance coefficient depends on the direction of the reflected beam and is defined by the ratio of the radiance reflected in this direction to the total incident irradiance. In general, the reflected radiance is not independent from the directional distribution of the incident radiation, which therefore has to be specified.

In the USA, the concept of bidirectional reflectance distribution function BRDF is similar to the radiance coefficient. The only difference is that the BRDF is a function of the directions of the incident and the reflected beam (Fig. 3). In detail, the (differential) irradiance dE_e impinging from a certain direction causes the reflected radiance dL_e in another direction, which is given by

dL_e = BRDF × dE_e

This BRDF depends on more arguments than the radiance coefficient. However, its advantage is the simultaneous description of the material’s reflection properties for all possible directional distributions of incident radiation, whereas the radiance coefficient is generally valid for just one specific directional distribution of incident radiation.

The unit of radiance coefficient and BRDF is 1/steradian. The BRDF is often abbreviated as the Greek letter ρ, which can easily be confused with the reflectance (see previous paragraph Reflectance ρ, Transmittance τ and Absorptance α).

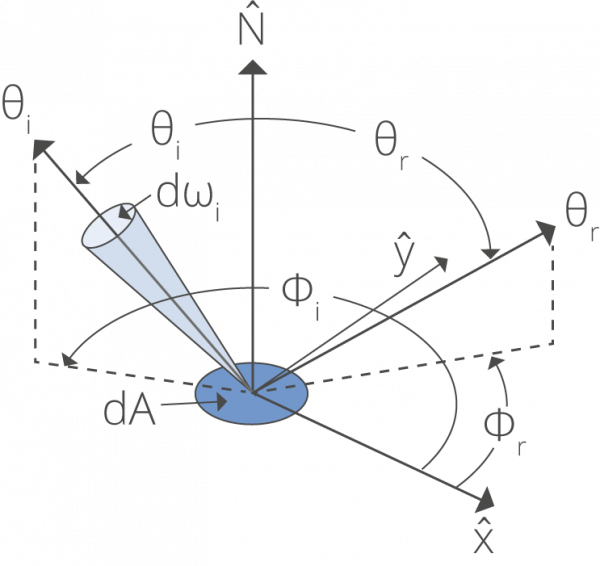
Fig. 3: Geometry used to define the bidirectional reflectance distribution function (BRDF).
The BRDF depends on the directions of incident and reflected radiation.
These are given by the angles ϑ_i and ϑ_r (which are measured in relation to the reflecting surface’s normal)
and the azimuth angles φ_i and φ_r, (which are measured in the plane of the reflecting surface)

Source (valid as of 2002): http://math.nist.gov/~FHunt/appearance/brdf.html